整理一下何錦文教授高等演算法課上的作業。
作業題目好像都不太會變的樣子?
所以如果你有參考我整理的題目的話,留個言讓我知道我做功德了♥
有什麼問題都可以在下面留言討論,私訊我也可以。
Written in English.
problem 1
Recall the recursive program (discussed in the class) that computes the n-th Fibonacci number. Compute the number of additions used by the program.
problem 2
Determine the space complexity of the quicksort algorithm.
The best case, it needs O(logn) recursive call to sort, the space complexity is O(logn).
The worse case, it needs O(n) recursive call to sort, the space complexity is O(n).
We know the the average case of quick sort is that it need O(logn) recursive call, so the space complexity of quicksort is O(logn).
problem 3
Derive an exact closed formula of the merge sort recurrence relation $T(n): T(n) = T(\lfloor \frac{n}{2} \rfloor) + T(\lceil \frac{n}{2} \rceil) + n-1, T(1) = 0$
problem 4
Given a set of n+1 numbers out of the first 2n natural numbers 1, 2, …, 2n, prove by mathematic induction that here are two numbers in the set, one of which divides the other.
Basis : $n = 1, 1|2 $
Assume that, for $n = k$, it holds(select k+1 numbers from first 2k natural numbers).
When $ n = k + 1 $(select k+2 numbers from first 2k+2 natural numbers), there are three situation:
Each number we select is less or equal to 2k, means that we select k+2 numbers from first 2k natural numbers. Under this situation, it holds.
One number we select is greater than 2k, means that we select remaining k+1 numbers from first 2k natural numbers. Under this situation, it holds.
We select both 2k+1 and 2k+2 :
- If we select k+1, then $(k+1)|(2k+2)$. It holds.
- If not, then it’s similar to the situation 2 ,which we select k+1 numbers from first 2k natural numbers.It means there exists $x|y$ in k+1 numbers we selected , if $ x \ne k+1, y \ne k+1 $,that means we can find $x|y$ in situation 3 without term k+1, but what if x or y equal to k+1 ? if $x|y,y=k+1$,it mean $x$ is ALSO a factor of 2k+2. It still holds.
$$ QED $$
problem 5
For an undirected graph $G=(V, E)$ and a vertex $v$ in $V$, let $G\backslash v$ denote the subgraph of $G$ obtained by removing $v$ and all the edges incident to $v$ from $G$. If $G$ is connected, prove that we can always find a vertex $v$ in $G$ such that $G\backslash v$ is connected.
Removing the leaf node of spanning tree still makes graph connected.
problem 6
Given $n \geq 1$ numbers x1, x2, …, xn, show that the function $f(x) = \sum_{1\le i\le n}|x-x_i|$ takes its minimum value at the median of these n number. Extend this result to the following problem: Given n pairs of numbers (a1, b1), …, (an, bn) with each $ ai \ne 0 $ , determine the position at which the function $ f(x) = \sum_{1\le i\le n}|a_ix-b_i| $ takes its minimum value.
$$let;M;=;median;of;x_i$$
$$ x_1 \le x_2 \le … \le x_s \le A \le x_{s+1} \le … \le x_t \le M \le x_{t+1} \le … \le x_n $$
- If n is even and an arbitrary number A is less or equal than M:
$$ n = 2t $$
$$ f(A) = {\sum_{i=1}^s(A-x_i) + \sum_{i=s+1}^n(x_i-A)}$$
$$ = \sum_{i=1}^t(A-M+M-x_i) - \sum_{i=s+1}^t(A-x_i)+\sum_{i=t+1}^n(x_i-M+M-A) +\sum_{i=s+1}^t(x_i-A)$$
$$ = \sum_{i=1}^t(M-x_i)+ t(A-M) + \sum_{i=t+1}^n(x_i-M)+(n-t)(M-A) + 2\sum_{i=s+1}^t(x_i-A)$$
$$ = \sum_{i=1}^t(M-x_i) + \sum_{i=t+1}^n(x_i-M) + 2\sum_{i=s+1}^t(x_i-A) +(n-2t)(M-A) $$
$$ when;A;=;M,;2\sum_{i=s+1}^t(x_i-A);has;minimum;value$$
(Proof this when A>=M,and when n is odd, it’s easy)
Extend this result to $ f(x) = \sum_{1\le i\le n}|a_ix-b_i| $
$Let;v_i=|a_i|,w_i=\frac{b_i}{a_i}$
$$f(x) = \sum_{1\le i\le n}|a_ix-b_i|$$
$$= \sum_{1\le i\le n}|a_i||x-\frac{b_i}{a_i}|$$
$$= \sum_{1\le i\le n}v_i|x-w_i|$$
$f(x) = \sum_{1\le i\le n}v_i|x-w_i|$ takes its minimum value at the median of the sequence :
$$w_1,w_1,…,w_1,…,w_2,w_2,…,w_2,…,w_n,w_n,…,w_n$$
$$|———v_1——–||———v_2—-|….|—–v_n——|$$
problem 7
Prove the Helly Property on Trees: Given a tree T and k subtrees of T such that each pair of subtrees has at least one vertex in common, show that there is at least one vertex in
common to all the subtrees.
Briefly, a set $J$ of sets $A_i$ has the Helly property if for every subset $T$ of $J$ the following holds: if the elements of $T$ pairwise intersect, then the intersection of all elements of $T$ is also non-empty.
![\[\]](/en/Advance-Algorithm-homework1/Helly.png)
Quoted from here
problem 8
Let $d_1, d_2, …, d_n,;n\le 2$, be positive integers. Prove that if $d_1+ d_2+ …+ d_n = 2n - 2$, then there exists a tree with n vertices of degrees exactly $d_1, d_2, …, d_n$. Based on your proof, design an efficient algorithm to construct such a tree.
Basis :
when $n=1,d_1=0$,it holds.
when $n=2,d_1=1,d_2=1$ , it holds.
Induction :
$$ Let;d_1\le d_2\le d_3\le … \le d_n $$
$$ d_1=1,otherwise, $$
$$ d_1+ d_2+ …+ d_n \ge 2n \ge 2n - 2 $$
$$ when;n\ne 2, d_n\ge 2,otherwise,$$
$$ d_1+ d_2+ …+ d_n = n < 2n-2 $$
Therefor
$$ d_1+ d_2+ …+ d_n +d_{n+1} = 2(n+1)-2 = 2n $$
$$ d_1+ d_2+ … + d_n +d_{n+1} - 2 = 2n-2 $$
$$ d_1+ d_2+ … + (d_n +d_{n+1} - 2) = 2n-2 $$
$ d_1+ d_2+ … + (d_n + d_{n+1} - 2) $ satisfy the induction hypothesis, so there exist a tree with n vertices with these degrees.
Remove $(d_{n+1} - 1)$ neighbours from the vertix whose degree is $(d_n + d_{n+1} - 2)$, connect those neighbours with a new node,and connect the new node with the vertix whose original degree is $(d_n + d_{n+1} - 2)$.
Then we get
$$ d_1+ d_2+ … + d_n +d_{n+1} = 2n $$
$$QED$$
algorithm :
- Sort $d_1+ d_2+ …+ d_n$ in ascending order.
- Create a node $P$ with smallest degree in sequence excluding 1.
- Iterating from 1 to n,and add nodes to $P$ until the degree of p become 1.
- Go back to 2 until there is no more nodes can be added
problem 9
Let G=(V, E) be a directed graph (not necessarily acyclic). Design an efficient algorithm to label the vertices of the graph with distinct labels from 1 to |V| such that the label of each vertex v is greater than the label of at least one of v’s predecessors, or determine that no such labeling is possible. (A predecessor of v is a vertex w such that $wv \in E$)
problem 10
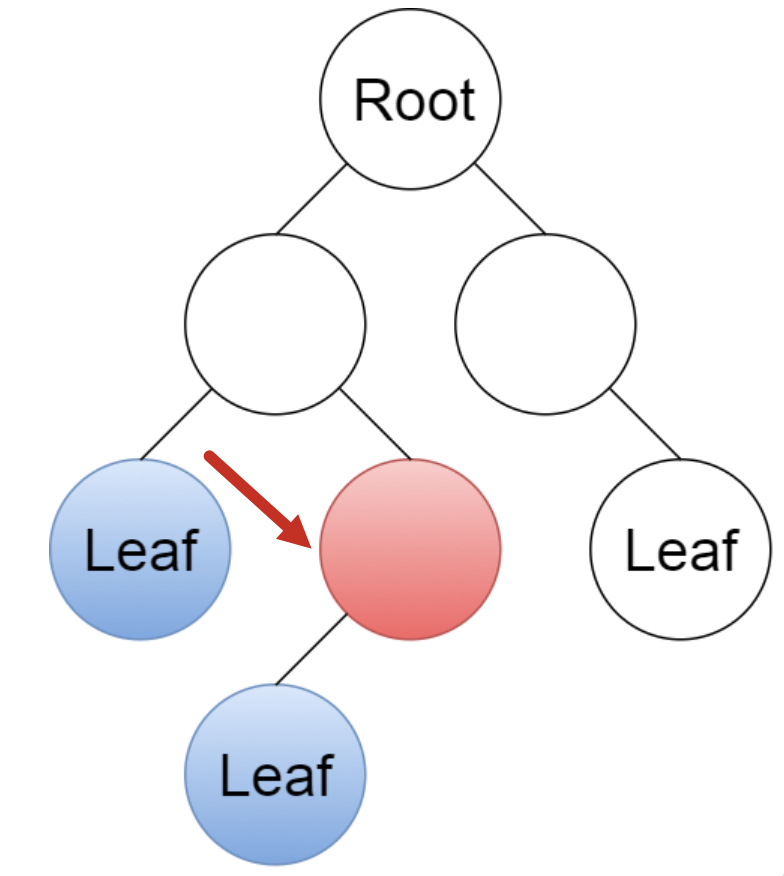
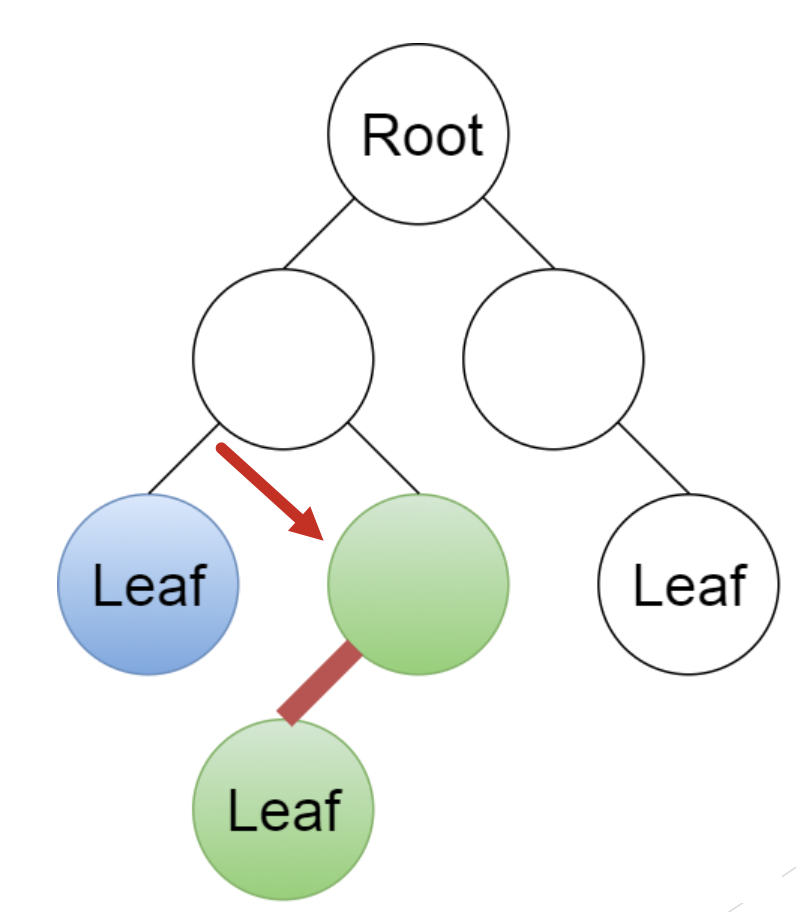
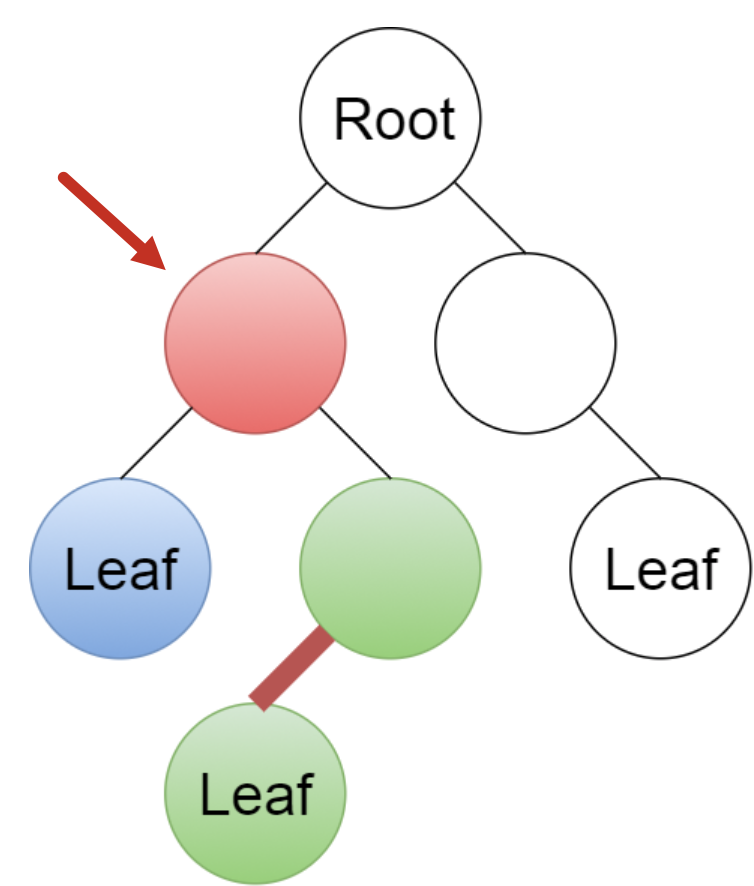
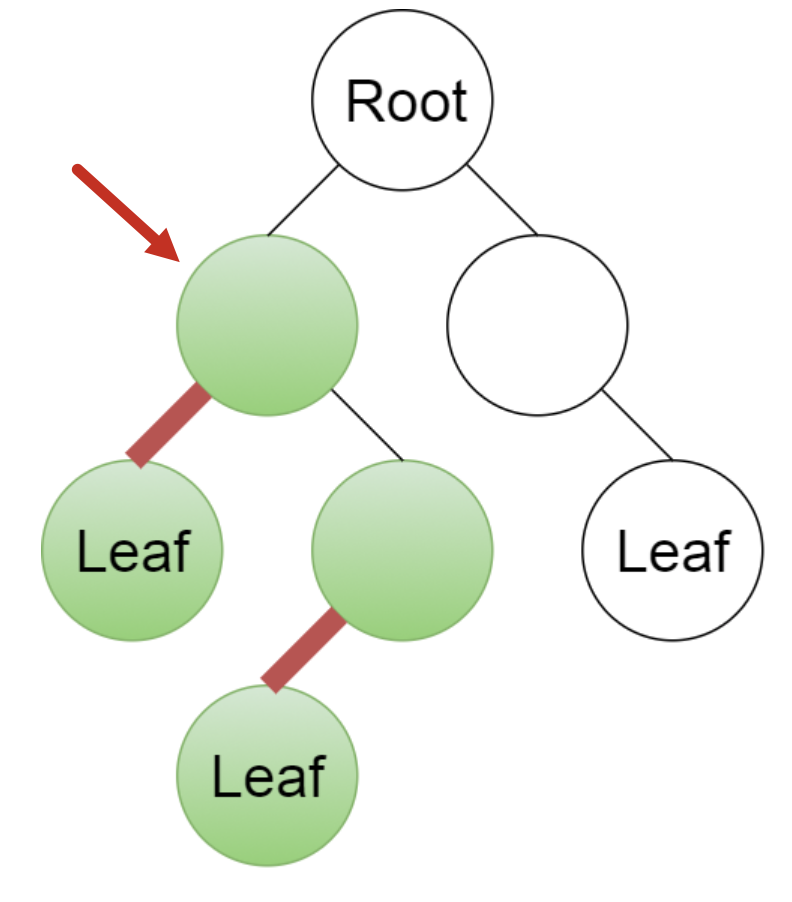
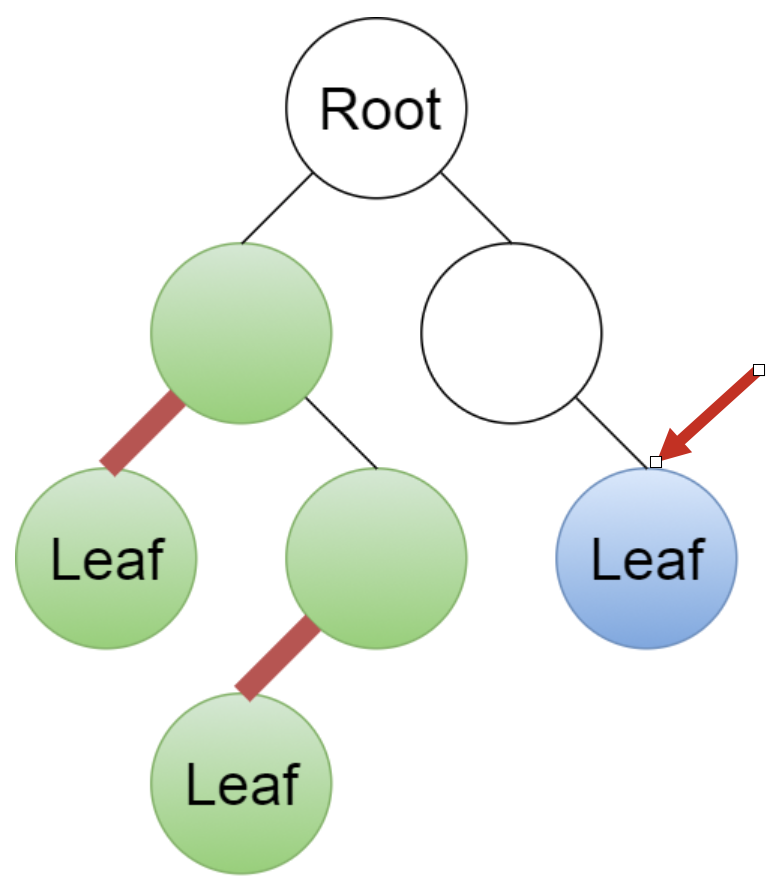
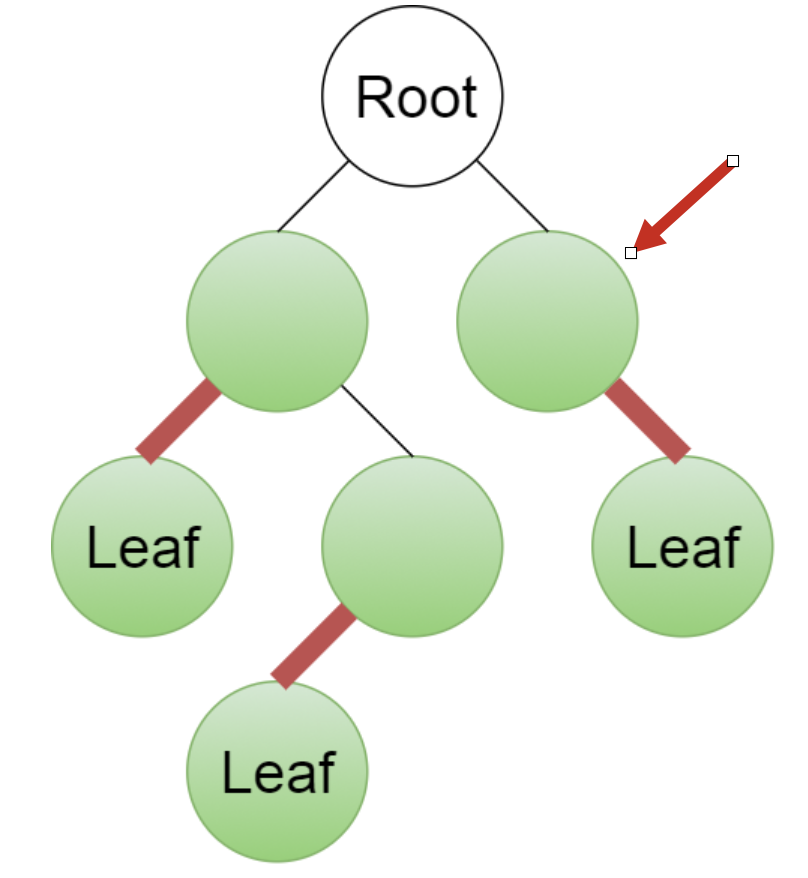
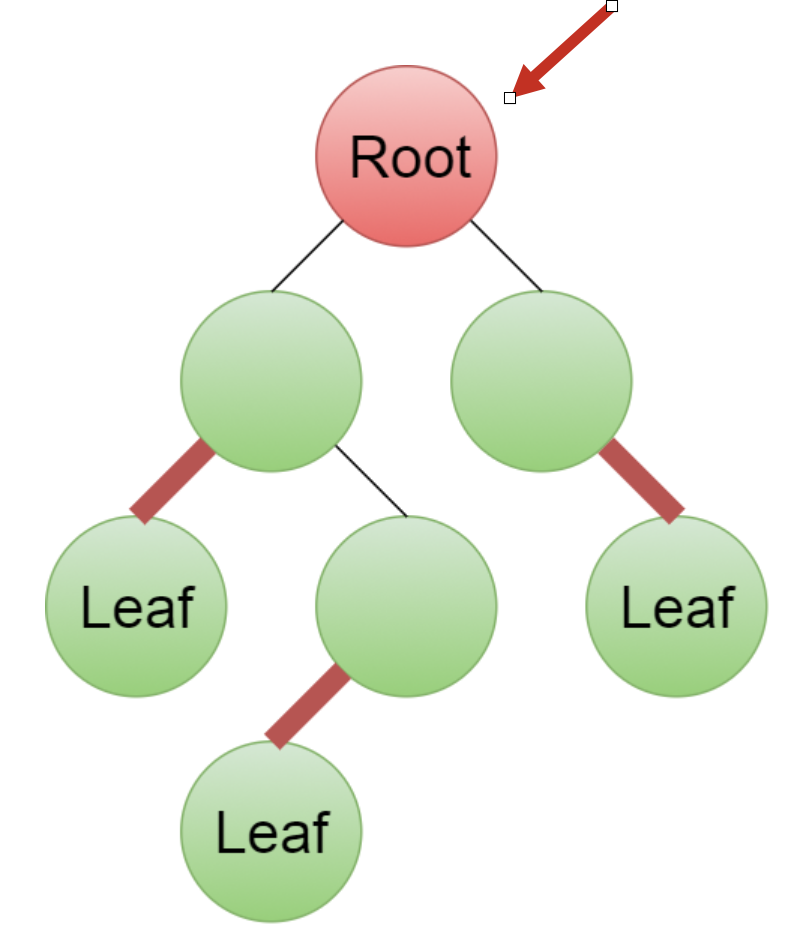
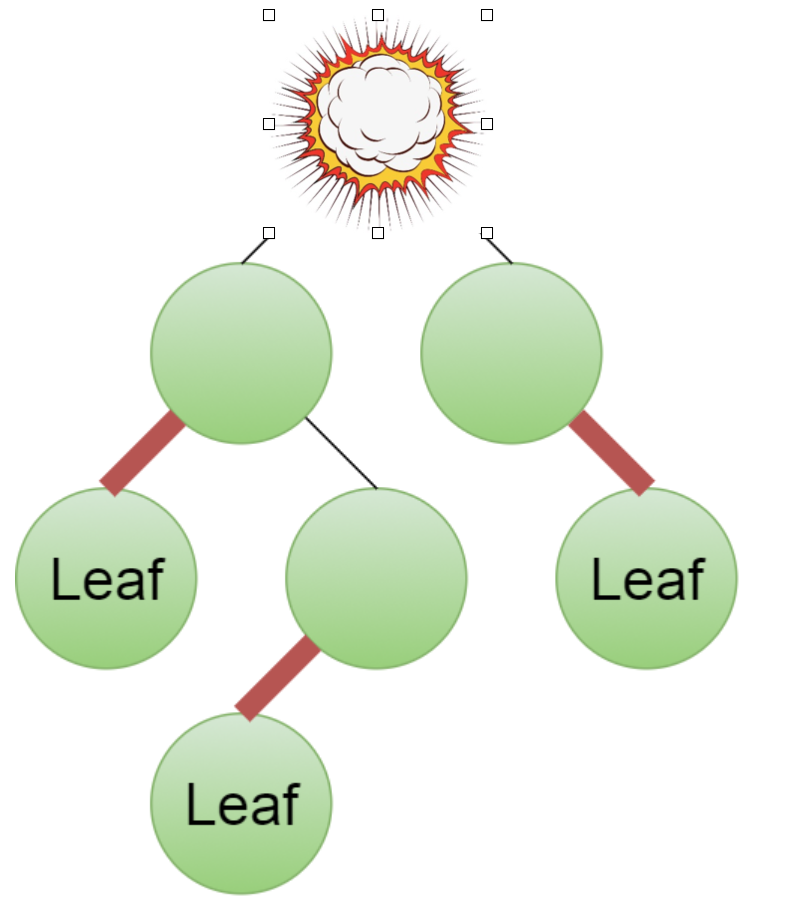
Give a linear-time algorithm that takes as input a tree and determines whether it has a perfect matching: a set of edges that touches each node exactly once.
Because leaf nodes must match with their parent, we can perform a devide and conquer algorithm.
 |
 |
 |
 |
 |
 |
 |
 |
|
problem 11
Consider a variation of the towers of Hanoi. We no longer assume that all the disks are initially on one peg. They may be arbitrarily distributed among the three pegs, as long as they are ordered in decreasing sizes on each peg. The purpose remains to move all disks to one specified peg, under the same constraints as the original problem, with as few moves as possible. Design an algorithm to find a minimal sequence of moves. How about the reverse of the problem?
Recursive Solution:
problem 12
Let T be an undirected tree. The distance between two vertices in T is the length of the path connecting these two vertices (neighbours have distance 1). The diameter of T is the maximal distance over all pairs of vertices. Design an algorithm to find the diameter of the given tree.
The algorithm look like this:
- Picking an arbitrary node, then find the farthest node $P_f$ from it.
- Next, find the farthest node $P_g$ from $P_f$.
- The distance between $P_g$ and $P_f$ is the diameter of T.
It’s easy to proof.
problem 13
Consider the iterative method for solving the towers of Hanoi problem described in Unit 2. Prove the correctness of the algorithm.
while (1) { |
Basis :
Induction :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
$$QED$$